Eukleidész görög matematikus Elemek cimű munkájában megfogalmazta alapigazságait (axiómáit). --<<a pont, egyenes, sík alapfogalmakat és talán alapvető viszonylatokat nem sorolja - FÁ>>--
A kilenc axióma:
1. Az egy és ugyanavval egyenlők egymással is egyenlők.
2. Ha egyenlőkhöz egyenlőket adunk, akkor az összegek is egyenlők.
3. Ha egyenlőkből egyenlőket veszünk el, akkor a maradékok is egyenlők.
4. Ha nem egyenlőkhöz egyenlőket adunk, az összegek nem egyenlőek.
5. Ugyanannak a kétszeresei is egyenlők.
6. Ugyanannak a fele részei is egyenlők.
7. Az egymással egybevágók egyenlők.
8. Az egész nagyobb a résznél.
9. Két egyenes nem fog közre területet.
Az axiómákat öt posztulátum (követelmény) követi: (Ezek a mai értelmezés szerint szintén axiómák)
1. Minden pontból minden ponthoz egyenes húzható.
2. Az egyenes szakasz végtelenül meghosszabbítható.
3. Minden pontból, mint középpontból tetszőleges sugarú kör rajzolható.
4. A derékszögek egyenlők.
5. Ha két, azonos síkban fekvő egyenes egy harmadik metsz, akkor a két egyenes a harmadiknak azon az oldalán metszi egymást, amelyiken a keletkezett belső szögek összege két derékszögnél kisebb.
Ez az utolsó posztulátum okozott gondot majd 2000 éven át a matematikusoknak. Elsősorban bonyolultsága és ellenőrizhetetlensége miatt. Ez indította el az axiómarendszerekre vonatkozó vizsgálatokat. És ezekből a kutatásokból, illetve a párhuzamossági axióma tagadásából született meg a Bolyai-Lobacsevszkij féle geometria. Ők ezt a páthuzamossági axiómát annak tagadásával helyettsítették:
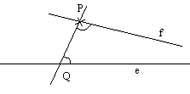
Az "e" egyeneshez egy külső P pontból több olyan egyenes húzható az "e" és P által meghatározott síkban, amely e-t nem metszi."
(A hiperbolikus geometria.)
A geometria axiomatikus felépítését. még az ókorban Eukleidész teremtette meg. Az ő általa kidolgozott euklideszi axiómarendszer ma is érvényes. Ebben az axiómarendszerben 9 axiómát és 5 posztulátumot (mai felfogás szerint ezek is axiómák) fogalmazott meg. Ezek között egyetlen egy van, amely régóta vita tárgya a matematikusok körében. Ez un. párhuzamossági axióma. Érdemes itt szó szerint is idézni:
|
" Ha két, azonos síkban fekvő egyenes egy harmadik metsz, akkor a két egyenes a harmadiknak azon az oldalán metszi egymást, amelyiken a keletkezett belső szögek összege két derékszögnél kisebb." |
|
Egyszerűbben: Egy egyeneshez egy külső ponton át egyetlen nem metsző egyenes húzható a pont és az egyenes által meghatározott síkban.
Ez a többi axiómánál bonyolultabb állítás arra inspirálta a matematikusokat, hogy ezt az axiómát többi axiómából levezessék (így már nem axióma, hanem bizonyított tétel lenne). Azonban ez senkinek sem sikerült.
Bolyai Farkas is azon az úton indult el, hogy a többi axiómából levezesse a párhuzamossági axiómát. Levezetésében azonban Gauss megtalálta a hibát. Ezek után megpróbálta más axiómával helyettesíteni: "Három pont vagy körön van, vagy egy egyenesen van."
Megjegyzés: Az euklideszi párhuzamossági axióma egyenértékű még azzal az állítással, hogy a háromszög szögeinek összege 180°.
Bolyai János 1820-ban kezdett a problémával foglalkozni, és 1823-ban írta édesapjának: "Semmiből egy új világot teremtettem."
Bolyai János és tőle függetlenül az orosz Lobacsevszkij a párhuzamossági axiómát annak tagadásával helyettesítették. Pontosabban:
" Az "e" egyeneshez egy külső P pontból több olyan egyenes húzható az "e" és P által meghatározott síkban, amely e-t nem metszi."
Ezek után mindketten megvizsgálták ennek következményeit, és az derült ki, hogy ez a helyettesítés nem vezet logikai ellentmondáshoz. Így, a módosított axiómarendszerrel egy új geometria született.
Természetesen ebben a geometriában is létezik párhuzamosság. Ezt a következőképpen értelmezzük:
|
A mellékelt ábrán a PB és QA félegyenesek a PQ egyenes ugyanazon oldalán vannak. PB és QA félegyenesek nem metszik egymást, azaz nincs közös pontjuk. A QPB szögtérben haladó és P-n átmenő minden egyenes metszi a QA-t. Ebben az esetben azt mondjuk, hogy a PB és QA félegyenesek párhuzamosak. |
|
|
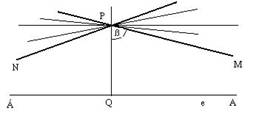
Ez a párhuzamosság-fogalom szemléletesen azt jelenti, hogy
ha elkezdjük forgatni a PQ egyenest A pont felé, akkor a
forgó félegyenes éppen "elpattanó", első nem metsző
helyzetében lesz párhuzamos QA-val. A mellékelt ábrán a PM
párhuzamos QA-val és PN párhuzamos QÁ-val. (mint "elpattanó
félegyenesek) Az új axióma azt mondja ki, hogy
több nem metsző egyenes van, tehát PM és PN nem esnek
egy egyenesbe. |
|
Ebben a geometriában (hiperbolikus geometriában) tehát a párhuzamosságot félegyenesekre értelmezzük. --<<Úgy tűnik nekem, hogy egészen egyértelműen hajózási rajz eszköz igényt tükröz a megfogalmazás. - FÁ>>-- Két egyenest akkor mondunk párhuzamosnak, ha vannak párhuzamos félegyeneseik.
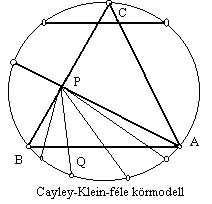
A hiperbolikus geometriáról szemléletes képet ad az un. Cayley-Klein-féle körmodell.
|
A hiperbolikus sík pontjait az un határkör belső pontjai jelentik. Két egyenes párhuzamos ("elpattanó"), ha a határkörön metszik egymást. Két egyenes ultrapárhuzamos, ha az egyeneseknek megfelelő húrok nem metszik egymást. A határkörbe írt háromszöget olyan egyenesek alkotják, amelyek közül bármelyik kettő párhuzamos a másik kettővel. (Ilyen az ábrán az ABC háromszög.) Ez a modell talán ilyen méretekben szokatlan, de csillagászati lépték esetén már nem. |
|
A Bolyai-Lobacsevszkij féle hiperbolikus geometria, mint speciális esetet tartalmazza az euklideszi geometriát is. Ma már tudjuk, hogy a fizikai tér nem euklideszi szerkezetű. Ugyanakkor a hiperbolikus geometriában feltételezettnél is bonyolultabb, nem jellemezhető egyetlen paraméterrel. A mi emberi világunk mértei és technikai feltételei között az euklideszi geometria elegendő pontossággal alkalmazható.
A Bolyai-Lobacsevszkij féle hiperbolikus geometria iránt érdeklődőknek nagyon ajánljuk a következő Internet címet: http://www.jgytf.u-szeged.hu/tanszek/matematika/Bolyai/index.html --<<Szilassi Lajos oldala - FÁ>>--
A fenti címen, a szegedi egyetem tanárképző főiskolai karának matematika tanszékén található Web oldalon találhatsz egy programot is (bolyai.exe), amely a hiperbolikus geometria ún. Poincaré-féle modelljét ábrázolja.
Peano 1889-ben jelentette meg az aritmetika alapjait jelentő axióma rendszerét.
Ebben három alapfogalmat mondott ki:
- a nulla,
- a nem negatív egész szám, és az
- azt követő
fogalmakat. Azaz a természetes számokat és a számlálást (rákövetkezést) alapfogalomnak tekintjük. Így 5 axióma (alapállítás) vált szimbólumokkal is leírhatóvá:
1. A nulla szám.
2. Ha a szám, akkor az azt követő is szám.
3. A nulla nem követi egyik számot sem.
4. Ha két szám ugyanazt a számot követi, akkor azok egyenlők.
5. Ha az S halmaz tartalmazza a nullát és az S minden számának a következőjét, akkor minden szám az S-ben van.
[D]
Hilbert,
David
(1862. 01. 23. -1943.
02. 14.)
Világhírű német matematikus. Königsbergben (ma Kalinyingrád) született. Gimnáziumi és egyetemi tanulmányait is itt végezte. Königberghez kötődik Goldbach, aki szintén itt született, és Euler a königsbergi hidak problémája kapcsán. 1895-ben a göttingeni egyetemre kerül és működött egészen haláláig. Itt az egyetemen többek között Félix Klein is kollégája volt. Hilbert tagja volt a Magyar Tudományos Akadémiának is, és 1910-ben ő kapta a világ legjobb matematikusai számára alapított Bolyai díjat.
Munkásságáról: Talán Hilbert az utolsó olyan matematikus, aki a matematika szinte valamennyi szakterületén nagyot alkotott. Munkássága kiterjedt az algebra, a számelmélet, a geometria, az analízis, a matematikai logika, a differenciálegyenletek, a variációszámítás és a topológia területeire. 1899-ben jelent meg híres könyve, a Grundlagen der Geometrie (A geometria alapja). Ebben általában is foglalkozik a matematika axiomatikus felépítésével. Ő fogalmazta meg, hogy melyek a helyes axióma-rendszer feltételei, és meg is adta a geometriának ma is használatos axiómarendszerét. Általánosította az euklideszi geometriát tetszőleges számú dimenzióra. Hilbert meg volt győződve arról, hogy a matematikában fellépő ellentmondások legyőzhetők. Egy ideig tanítványai közé tartozott a nagy magyar származású matematikus, Neumann János.
[E] Halmazelmélet axiómarendszere.
A matematika axiómatikus felépítése és a matematika fejődésében jelentős állomás volt a halmazelméleti axiómarendszer megfogalmazása. Ez először 1908-ra alakult ki Ernst Friedrich Ferdinand Zermelo (1871.-1953.) német és Adolf Abraham Fraenkel (1891.-1965.) izraeli matematikusok munkássága nyomán. Ebben a rendszerben halmazok elemeiként is csak halmazok jöhetnek számításba.
Zermelo-Fraenkel féle axiómarendszer.
Alapfogalmak:
1. A halmaz fogalma.
2. Halmaz elemének lenni. (Halmazhoz tartozás.)
Axiómák:
1. Ha két halmaz elemei ugyanazok, akkor a két halmaz azonos.
2. Van olyan halmaz, amelynek nincs eleme. Ez az üres halmaz: Æ ={}.
3. Ha a és b halmazok, akkor van olyan halmaz, amelynek pontosan a és b az elemei. Ez {a,b} halmaz, illetve ha a=b, akkor az {a} halmaz.
4. Van olyan halmaz, amelynek eleme Æ , és ha egy a halmaz eleme neki, akkor az {a} halmaz is eleme. (végtelen halmaz létezése).
5. Bármely halmazhoz van olyan halmaz, amely az adott halmaz elemeinek az egyesítése.
6. Minden halmaznak létezik hatványhalmaza. (Hatványhalmaz: egy adott halmaz összes részhalmazaiból álló halmaz.)
7. Ha A egy halmaz és T egy tulajdonság, amely a halmazelmélet fogalmaival definiálható, akkor létezik az A halmaz T tulajdonságú elemeinek a halmaza.
8. Ha A egy halmaz és f egy olyan függvény, amely a halmazelmélet fogalmaival definiálható, akkor, értelmezési tartománya az A halmaz, akkor az f függvény értékkészlete is halmaz.
9. Nem üres halmaznak mindig van tőle idegen eleme.
10. Ha egy A halmaz elemei páronként diszjunkt (közös rész nélküli) nem üres halmazok, akkor létezik olyan B halmaz, amelynek A halmaz minden elemével pontosan egy közös eleme van. (Kiválasztási axióma.)
Megjegyzés: Ez utóbbi axióma hasonló szerepet játszik, mint az euklideszi axiómáknál a párhuzamossági axióma.
Az idők során fogalmazódtak meg más axiómarendszerek is, például Neumann Jánosé. Ezek egyenértékűek a fenti axiómarendszerrel. Neumann János axiómarendszere azonban nem a "halmaz" és az "eleme" alapfogalmakra épül, hanem ezt a szerepet a "függvény" és az "argumentum" fogalmak veszik át.